АКАДЕМИЯ НАУК СССР

     1979 ТРУДЫ ОРДЕНА ЛЕНИНА ФИЗИЧЕСКОГО ИНСТИТУТА им. П. Н. ЛЕБЕДЕВА
     Том 110

     А. Р. СПЕКТОР

     ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ГИДРОДИНАМИКИ ПРОЗРАЧНОЙ ПЛАЗМЫ ПРИ ИМПУЛЬСНОМ НАГРЕВЕ ЭЛЕКТРОНАМИ СО СТЕПЕННЫМ СПЕКТРОМ

     Задача о гидродинамике оптически прозрачной плазмы при нагреве ее пучком электронов была сформулирована в [1]. Здесь мы рассмотрим особенности задачи, создающие трудности ее численного решения, и обсудим методы их устранения. Итак, исходной является система четырех уравнений в безразмерном виде:

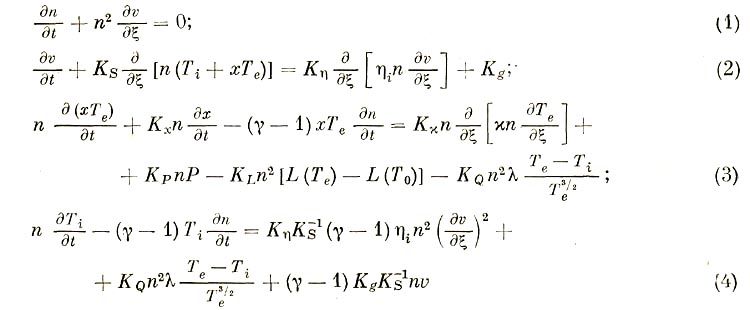
     с начальными

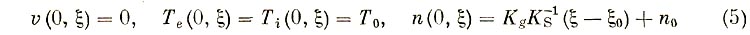
     и граничными условиями

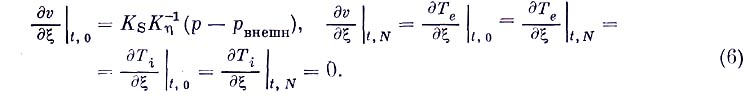
     Здесь индексы 0, N обозначают соответственно верхнюю и нижнюю границы рассматриваемой области. Остальные обозначения и физический смысл пояснены в [2, 3].

     1. Разностные схемы и метод счета

     После замены 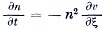и подстановки значении некоторых функций исходные уравнения примут вид:

     1) уравнение непрерывности

     2) уравнение движения

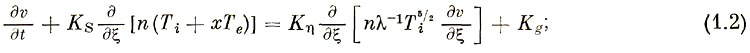
     3) уравнение для электронной температуры

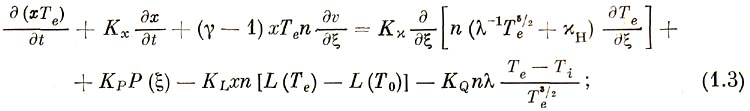
     4) уравнение для ионной температуры

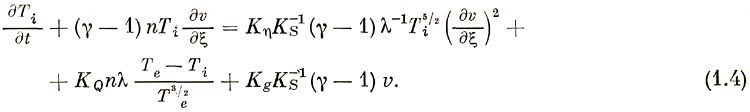
     Для этих уравнений составляются разностные схемы: 1) уравнение непрерывности

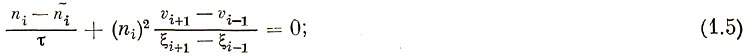
     2) уравнение движения

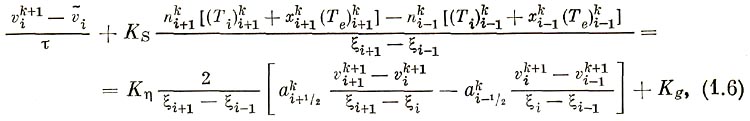
где

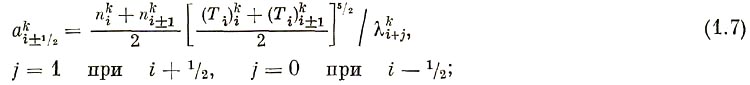
     3) уравнение для электронной температуры

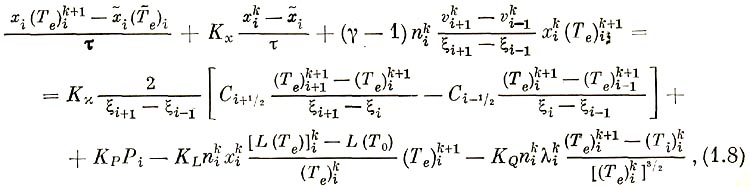
где

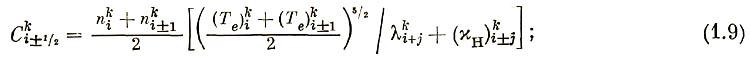
     4) уравнение для ионной температуры

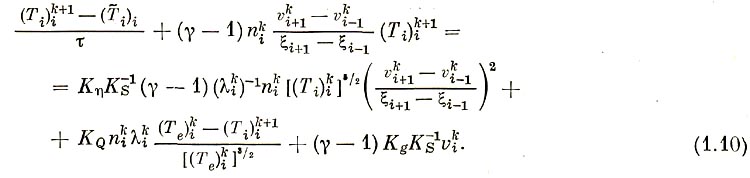
     Здесь и в дальнейшем нижний индекс относится к пространственному шагу, верхний индекс обозначает номер итерации. Тильдой обозначается значение функции с предыдущего шага по времени, при первой итерации в качестве значения предыдущей итерации используется значение с предыдущего шага по времени, τ - шаг по времени.

     Уравнение для электронной температуры и уравнение движения решаются методом прогонки с итерациями, уравнение для ионной температуры - прямым методом с итерациями, а уравнение непрерывности без итераций как квадратное уравнение относительно n_i . Кроме того, проводится итерирование по всей системе уравнений сравнением значений электронной температуры. Итерации ограничивались следующим выражением:

     2. Расчеты элементарных процессов

     Приведенная система уравнений (1) - (4) с начальными и граничными условиями (5), (6) при ее решении разностным методом не поддается точной проверке полученных результатов независимым методом. Поэтому были выполнены расчеты отдельных физических процессов; это обеспечивалось приравниванием нулю в программе всех членов уравнений, кроме одного или нескольких, для которых проводилась данная проверка. Такие проверки позволяют быть уверенными в правильности окончательных результатов.

     Нагрев хромосферы, энергичными частицами в данной задаче является основным физическим процессом, который вызывает все остальные явления. Для проверки правильности работы программы исключим из рассмотрения все уравнения, кроме уравнения электронной температуры. Кроме того, положим равными нулю следующие безразмерные коэффициенты: К_x , К_Q , K_L , и положим x = 1. Таким образом,

     Результаты машинного счета такого примера приведены на рис. 1. С другой стороны, уравнение (2.1), очевидно, имеет решение

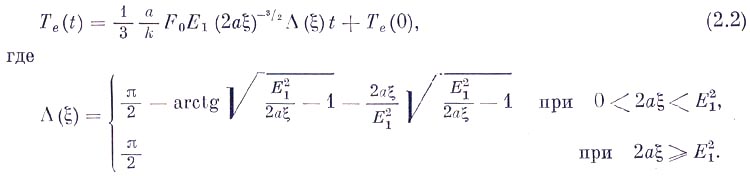
     Сравнение результатов численного счета с аналитическим решением (2.2) показывает полное совпадение результатов. Вычисляли также интеграл для

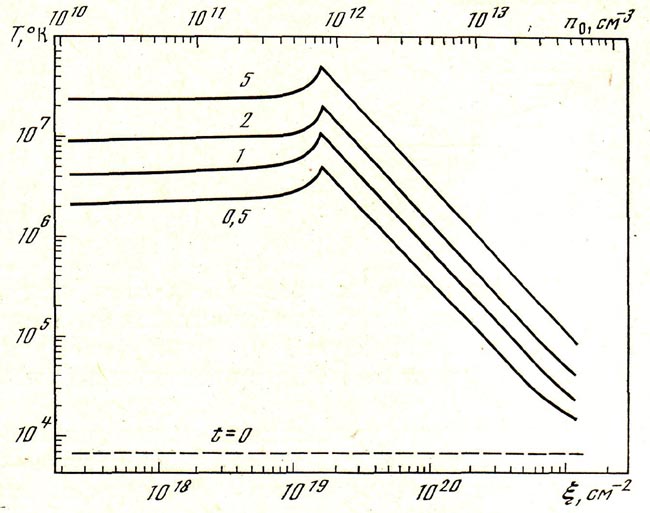
     Рис. 1. Проверка функции нагрева хромосферы пучком ускоренных электронов
     Приравнены нулю безразмерные коэффициенты Κ_x = К_Q = =K_L = 0

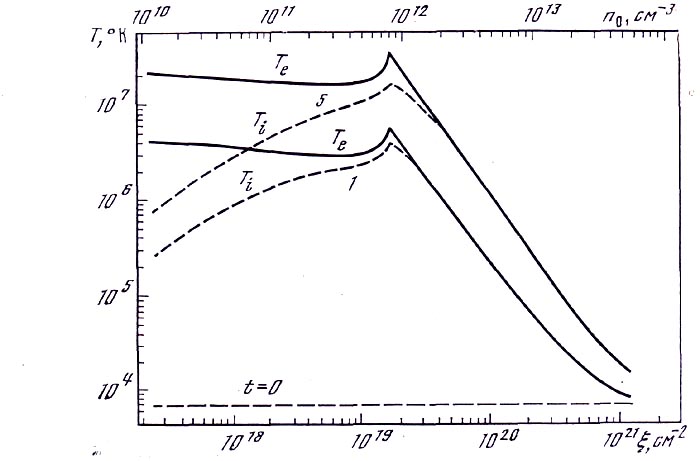
     Рис. 2. Проверка функции обмена энергией между ионами и электронами К_х = = K_L = 0

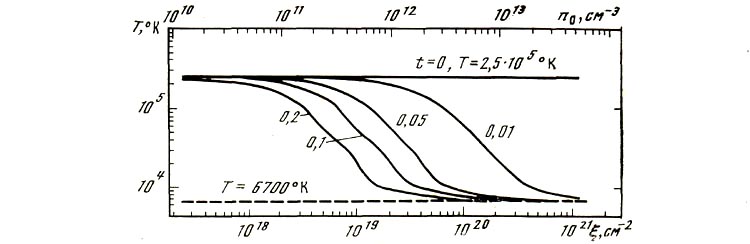
     Рис. 3. Проверка функции охлаждения хромосферы излучением, К_х = = K_Q = К_P =0

     каждого момента времени

     Кроме того, проводилась такая же проверка с верхней границей спектра частиц при Е2 = 50 кэв. В этом случае вся энергия пучка частиц выделяется на рассматриваемом нами участке хромосферы и можно сравнить полную энергию быстрых частиц с изменением температуры на этом участке:

     Проверка показала, что и это условие при расчетах выполняется полностью. Обмен энергией между электронами и ионами проверяется решением уравнений электронной и ионной температур с равными нулю коэффициентами

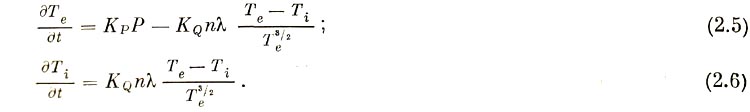
     Результаты расчета приведены на рис. 2. Для проверки в нескольких точках численные значения электронной температуры из предыдущего примера

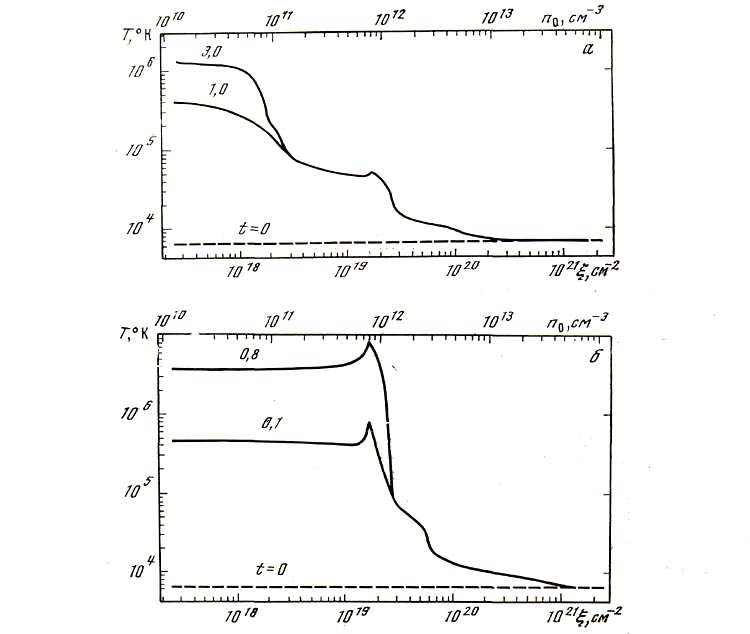
     Рис. 4. Проверка функций нагрева при F_o = 10¹⁰ (а) и 10¹¹ эрг см^-2· сек^-1 (б) и охлаждения излучением с установлением равновесного профиля К_x = = K_Q = 0

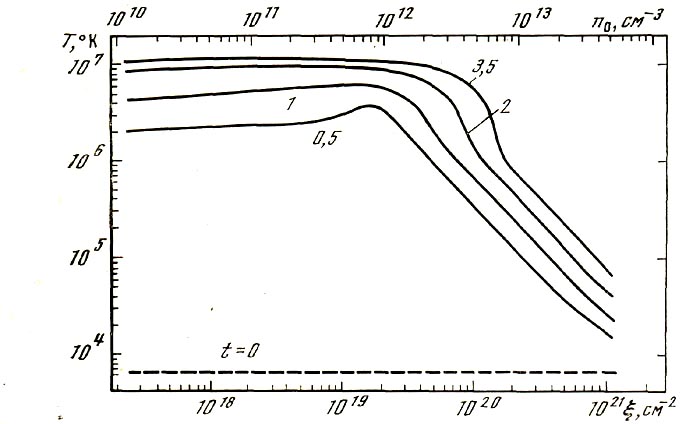
     Рис. 5. Проверка функции теплопроводности,

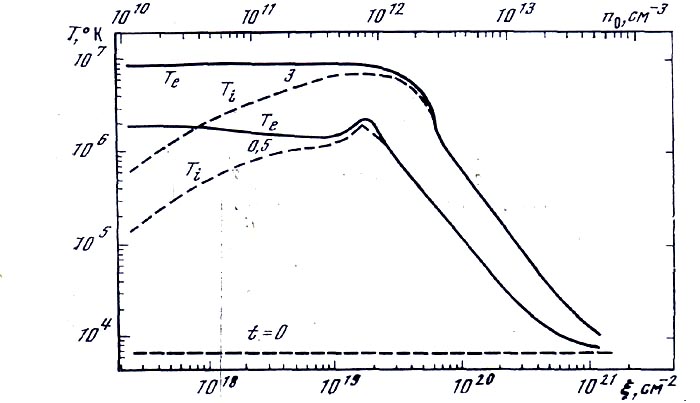
     Рис. 6. Проверка одновременного действия функции нагрева, теплопроводности и обмена энер-гиеймежду ионами и электронами, К_х = K_L = 0

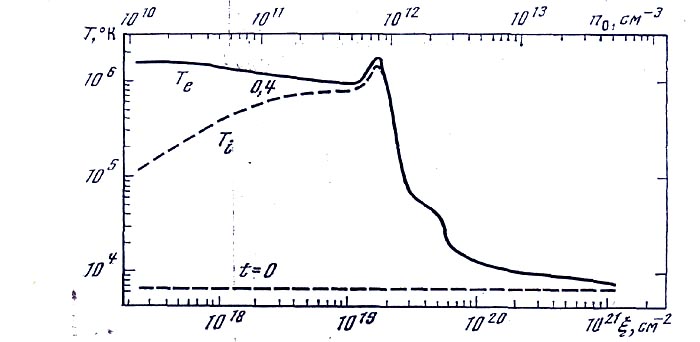
     Рис. 7. Проверка одновременного действия всех физических процессов в стационарной атмосфере

сравнивались с суммой электронной и ионной температур в настоящем примере. Вычисляли также интеграл

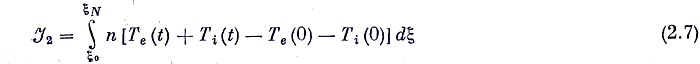
и сравнивали 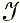₂ = 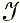₁   в одинаковых моментах времени.

     Для проверки правильности счета охлаждения излучением решали уравнение электронной теплопроводности (3) с равными нулю коэффициентами K_x , , K_Q , K_P , a именно уравнение

     При этом задавалась первоначальная температура T_e = 2,5 10⁵ °К, что соответствует максимуму функции потерь энергии на излучение (рис. 3). Из-за неравномерностей этой функции для проверки здесь следует повторить машинные действия по шагам с размерными величинами. Проведенные расчеты для момента времени t = 0,1 сек показали правильность работы этой части программы.

     Кроме того, проводилась проверка при одновременном нагреве электронами и охлаждении излучением, т. е. решалось уравнение электронной теплопроводности с равными нулю коэффициентами K_x , , K_Q , т. е.

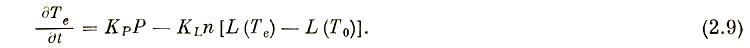
     Как легко видеть, при малых значениях Ρ ж в областях с большой плотностью при Т_е 2,5·10⁵ °К должно установиться равновесие, т. е. вся энергия, получаемая от нагрева электронами, немедленно излучается:

     Численно такие сравнения проводились для двух различных мощностей граничного потока энергии электронов: F_o = 10¹⁰ (рис. 4, а) и 10¹¹ эрг·см^-2· • сек^-1 (рис. 4, б). Затем по рассчитанным значениям электронной температуры Те и известным значениям ξ, n в нескольких точках проводили расчет значения потерь энергии на излучение и сравнение с вкладом энергии электронов в той же точке.

     Теплопроводность проверялась решением уравнения (3) с равными нулю коэффициентами К_x, К_Q, К_L (рис. 5)

     Вычислялся интеграл 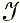₁ (2.3) и сравнивался с таким же интегралом в отсутствие теплопроводности, т. е. при К_x = 0 (рис. 1). Интегралы совпадали, что и следовало ожидать в силу граничного условия (6).

     Проверялось также одновременное действие теплопроводности и ионной температуры, т. е. решались уравнения для электронной и ионной компонент с равными нулю коэффициентами К_x , К_Q , К_L (рис. 6):

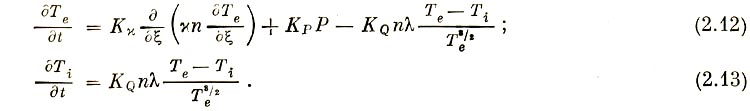
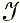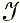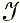     Здесь вычислялся интеграл ₂ и сравнивались ₂ = ₁.

     Взаимодействие отдельных физических процессов проверялось решением уравнений для электронной и ионной температур в неизменном виде (рис. 7) при :

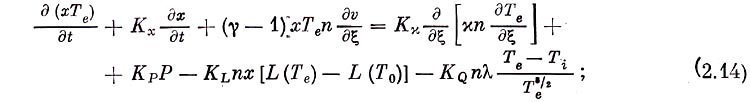
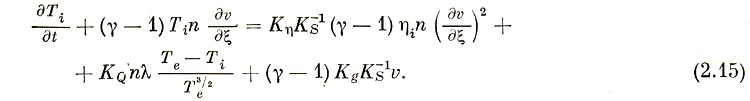
     При этом вычислялась сумма интегралов

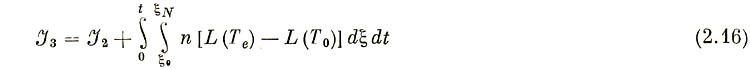
и проверялось равенство ₃ = ₁.

     В пределах точности счета все проведенные проверки дают правильные результаты.

     3. Исследование неустойчивости

     Сначала были проведены предварительные расчеты с однородной в логарифмическом масштабе по ξ сеткой, состоящей из 101 точки, и с достаточно малым шагом по времени, который оценивался в соответствии с обычными критериями устойчивости разностной схемы для гиперболической части системы уравнений. Наиболее ограничительная часть условий устойчивости, связанная с параболической частью системы, снималась применением обычного метода прогонки по аналогии с [4]. Тем не менее уже при малых значениях времени (t 0,5 сек) в области уплотнения вещества (конденсации) под вспышечным переходным слоем возникала неустойчивость численного характера, которая быстро нарастала и препятствовала проведению дальнейшего счета.

     Чтобы выявить причину неустойчивости, пространственный шаг сетки был уменьшен в 10 раз в области, отмеченной буквой А на рис. 8. Наиболее интересная часть результатов счета (область В на рис. 9) представлена отдельно на рис. 10 в момент времени t = 0,5 (непосредственно перед возникновением неустойчивости) и 0,75 сек (сразу же после начала неустойчивости). Результаты расчета с очевидностью демонстрируют, что неустойчивость возникает на той части растущей конденсации, которая обращена в глубь хромосферы. Неустойчивость имеет пилообразный характер и не связана с возбуждением сеткой возмущений конденсационного типа, ибо в таких возмущениях приращения температуры и плотности имели бы противоположные знаки. Растущие возмущения не связаны и со звуковой модой тепловой неустойчивости [3], поскольку они наблюдаются при температурах, меньших, чем необходимые для развития звуковой моды. Рис. 10, б, на котором представлены профили скорости, позволяет сделать предположение, что возникновение численной неустойчивости совпадает с моментом времени и местом формирования ударной волны, которая появляется в результате сверхзвукового движения конденсации в глубь хромосферы. В момент времени t = 0,5 сек скорость движения конденсации достигает ~100 км/сек, что соответствует числу Маха M ~ 10. Однако профиль скорости впереди конденсации еще достаточно гладкий, занимает более десяти шагов сетки, ударная волна еще не сформировалась. Напротив, в момент времени t = 0,75 сек, хотя профиль скорости и искажен пилообразной неустойчивостью, видно, что он более крутой, чем в предыдущий момент. Если предполагать, что в момент времени t = 0,75 сек в решении присутствует ударная волна, то ширина ее фронта сравнима с длиной свободного пробега в плазме и заведомо на много порядков меньше, чем шаг сетки в области неустойчивости. В пользу этого предположения свидетельствуют также результаты расчета, выполненного с шагом сетки, уменьшенным еще в 2 раза,- неустойчивость сохраняется, имеет пи-

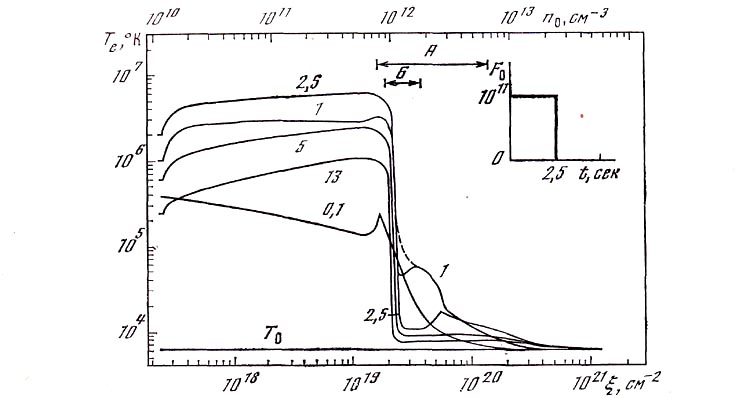
     Рис. 8. Распределение электронной температуры T_e по толще вещества ξ в примере счета с учетом динамических процессов
     Буквой А отмечена область дробления шага в случае расчетов без искусственной вязкости

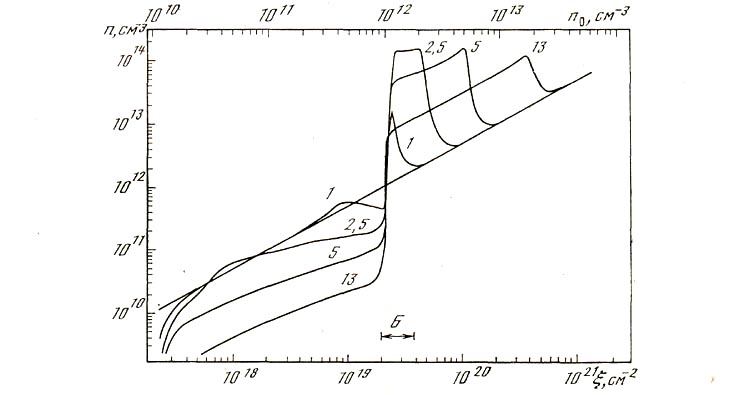
     Рис. 9. Профили концентрации при условиях, соответствующих рис. 8
Буквой Б отмечена область, которая в более увеличенном масштабе показана на рис. 10

лообразную структуру приблизительно с шагом сетки и "привязана" к переднему краю профиля скорости. Поэтому был сделан вывод, что неустойчивость, препятствующая счету, имеет вычислительный характер и обусловлена наличием узкого фронта ударной волны в хромосфере перед движущейся конденсацией вещества.

     Численная неустойчивость была устранена введением искусственной вязкости [4, 5]

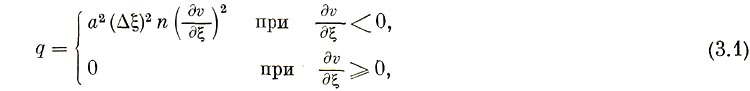
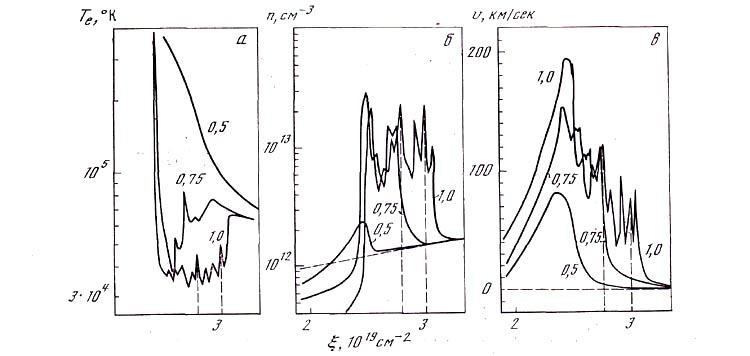
     Рис. 10. Возникновение неустойчивости счета в момент формирования ударной волны перед движущейся в глубь хромосферы конденсацией

     размазывающей фронт ударной волны на η шагов сетки при а = 2. После этого отпала необходимость в уменьшении шага сетки в области Ä, и все расчеты были выполнены с равномерной в логарифмическом масштабе по толще вещества сеткой и n = 4.

     Распространяющаяся в глубь хромосферы ударная волна сжимает ее, что в свою очередь увеличивает скорость лучистого охлаждения и приводит к росту массы конденсации. На этот процесс, т. е. тепловую неустойчивость за фронтом сильной ударной волны в плазме с космическим обилием элементов, первыми обратили внимание авторы работы [6], которые рассматривали модель начальной фазы хромосферной вспышки в рамках теории высокотемпературного взрыва в однородной атмосфере и численно решали одномерную (сферически-симметричную) систему уравнений газодинамики полностью ионизированной двухтемпературной плазмы с учетом потерь на излучение и всех существенных диссипативных процессов (подробнее о [6] см. в [1]).

     Заключение

     Численное моделирование гидродинамики прозрачной плазмы при нагреве энергичными электронами предполагает учет характерных особенностей, появляющихся в среде, излучательная способность которой сложным образом зависит от температуры. Наиболее важной из этих особенностей является образование холодной конденсации под вспышечным переходным слоем и одновременное ее движение в глубь хромосферы при распространении ударной волны в среду с экспоненциально возрастающей плотностью. Эта конденсация возникает и развивается вследствие тепловой неустойчивости и создает уплотнение вещества в тонком слое более чем на два порядка. Перепад температур во вспышечном переходном слое составляет около трех порядков (T_мах 10⁷ °К, Т_тiп 10⁴ °К). Скорость движения ударной волны в глубь хромосферы достигает ~150 км/сек.

     Приведенные особенности при вычислениях на ЭВМ создают неустойчивость численного характера. Она была устранена введением искусственной вязкости. Большая плотность в конденсации вызывает также необходимость пользоваться очень маленьким значением шага по времени (τ 10^-3 сек). Проведенные расчеты отдельных физических процессов показали правильность численного счета.

     Автор выражает благодарность Б. В. Сомову и С. И. Сыроватскому за руководство работой и Б. Я. Мартузану за неоднократные обсуждения и консультации по численным методам.

     ЛИТЕРАТУРА

     1. Сомов Б. В., Сыроватский С. И. - УФН, 1976, 120, с. 217-257.
     2. Сомов Б. В., Спектор А. Р., Сыроватский С. И. - Наст. сборник, с. 73-94.
     3. Сомов Б. В., Спектор А. Р., Сыроватский С. И. - Изв. АН СССР. Сер. физ., 1977,. 41, № 2, с. 273-287.
     4. Рихтмайер Р. Д. Разностные методы решения задач математической физики. М.: Мир, 1960.
     5. Годунов С. К., Рябенький В. С. Разностные схемы. М.: Мир, 1973.
     6. Гусейнов Р. Э., Имшенник В. С, Палейчик В. В. - Астрон. журн., 1971, 48, с. 1217 - 1226.